

NOT having sufficient data to ascertain the exact degree of propelling power exerted by birds in the act of flying, it is uncertain what degree of energy may be required in this respect in vessels for aerial navigation: yet, when we consider the many hundred miles of continued flight exerted by birds of passage, the idea of its being only a small effort is greatly corroborated. To apply the power of the first mover to the greatest advantage in producing this effect, is a very material point. The mode universally adopted by nature is the oblique waft of the wing. We have only to choose between the direct beat overtaking the velocity of the current, like the oar of a boat; or one, applied like the wing, in some assigned degree of obliquity to it. Suppose 35 feet per second to be the velocity of an aerial vehicle, the oar must be moved with this speed previous to its being able to receive any resistance; then, if it be only required to obtain a pressure of 1/10-th of a pound upon each square foot, it must exceed the velocity of the current 7.5 feet per second. Hence its whole velocity must be 42.5 feet per second. Should the same surface be wafted downward, like a wing, with the hinder edge inclined upward in an angle of about 50¡ 40' to the current, it will overtake it at a velocity of 3.5 feet per second; and as a slight unknown angle of resistance generates a pound pressure per square foot at this velocity, probably a waft of little more than 4 feet per second would produce this effect; one tenth part of which would be the propelling power. The advantage in favour of this mode of application, compared with the former, is rather more than ten to one.
In combining the general principles of aerial navigation for the practice of the art many mechanical difficulties present themselves, which require a considerable course of skilfully applied experiments, before they can be overcome. But to a certain extent the air has already been made navigable; and no one, who has seen the steadiness with which weights to the amount of ten stone (including four stone, the weight of the machine) hover in the air, can doubt of the ultimate accomplishment of this object.
The first impediment I shall take notice of is the great proportion of power, that must be exerted previous to the machine's acquiring that velocity, which gives support upon the principle of the inclined plane; together with the total want of all support during the return of any surface used like a wing. Many birds, and particularly water fowl, run and flap their wings for several yards before they can gain support from the air. The swift (hirundo apus Lin.) is not able to elevate itself from level ground. The inconvenience under consideration arises from very different causes in these two instances. The supporting surface of most swimming birds does not exceed the ratio of 4/10-ths of a square foot to every pound of their weight: the swift, though it scarcely weighs an ounce, measures eighteen inches in extent of wing. The want of surface in the one case, and the inconvenient length of wing in the other, oblige these birds to aid the commencement of their flight by other expedients; yet they can both fly with great power, when they have acquired their full velocity.
A second difficulty in aerial navigation arises from the great extent of lever, which is constantly operating against the first mover, in consequence of-the distance of the centre of support in large surfaces, if applied in the manner of wings.
A third and general obstacle is the mechanical skill required to unite great extension of surface with strength and lightness of structure; at the same time having a firm and steady movement in its working parts, without exposing unnecessary obstacles to the resistance of the air. The first of these obstacles, that have been enumerated, operates much more powerfully against aerial navigation upon a large scale, than against birds; because the small extent of their wings obliges them to employ a very rapid succession of strokes, in order to acquire that velocity which will give support; and during the small interval of the return of the wing, their weight is still rising, as in a leap, by the impulse of one stroke, till it is again aided by another. The large surfaces that aerial navigation will probably require, though necessarily moved with the same velocity, will have a proportionably longer duration both of the beat and return of the wing; and hence a greater descent will take place during the latter action, than can be overcome by the former.
There appears to be several ways of obviating this difficulty. There may be two surfaces, each capable of sustaining the weight, and placed one above the other, having such a construction as to work up and down in opposition when they are moved, so that one is always ready to descend, the moment the other ceases. These surfaces may be so made, by a valvelike structure, as to give no opposition in rising up, and only to resist in descent.
The action may be considered either oblique, as in rotative flyers; alternately so, without any up and down waft, as in the engine I have ascribed to Mr. Degen; by means of a number of small wings in lieu of large ones, upon the principle of the flight of birds, with small intervals of time between each waft; and lastly by making use of light wheels to preserve the propelling power both of the beat and the return of the wings, till it accumulates sufficiently to elevate the machine, upon the principle of those birds which run themselves up. This action might be aided by making choice of a descending ground like the swift.
With regard to another part of the first obstacle I have mentioned, viz. the absolute quantity of power demanded being so much greater at first than when the full velocity has been acquired; it may be observed, that, in the case of human muscular strength being made use of, a man can exert, for a few seconds, a surprising degree of force. He can run up stairs, for instance, with a velocity of from 6 to 8 feet perpendicular height per second, without any dangerous effort; here the muscles of his legs only are in action; but, for the sake of making a moderate statement, suppose that with the activity of his arms and body, in addition to that of his legs, he is equal to raising his weight 8 feet per second; if in this case he weighs 11 stone, or 154 pounds, he will be exerting, for the time, an energy equal to more than the ordinary force of two of Messrs. Boulton and Watt's steam horses; and certainly more than twelve men can bestow upon their constant labour.
If expansive first movers be made use of, they may be so constructed, as to be capable of doing more than their constant work; or their power may be made to accumulate for a few moments by the formation of a vacuum, or the condensation of air, so that these expedients may restore at one time, in addition to the working of the engine, that which they had previously absorbed from it.
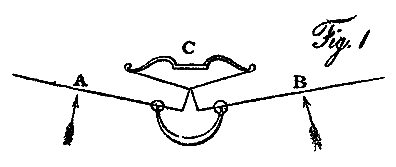
With regard to the second obstacle in the way of aerial navigation, viz. the length of leverage to which large wing like surfaces are exposed, it may be observed, that, being a constant and invariable quality, arising from the degree of support such surfaces give, estimated at their centres of resistance, it may be balanced by any elastic agent, that is so placed as to oppose it. Let A and B, Pl. IV, fig. 1, be two wings of an aerial vehicle in the act of skimming; then half the weight of the vessel is supported from the centre of resistance of each wing; as represented by the arrows under them. If the shorter ends of these levers be connected by cords to the string of a bow C, of sufficient power to balance the weight of the machine at the points A and B, then the moving power will be left at full liberty to produce the waft necessary to bend up the hinder edge of the wing, and gain the propelling power. A bow is not in fact an equable spring, but may be made so by using a spiral fusee. I have made use of it in this place merely as the most simple mode of stating the principle I wished to exhibit. Should a counterbalancing spring of this kind be adopted in the practice of aerial navigation, a small well polished cylinder, furnished with what may be termed a bag piston (upon the principle made use of by nature in preventing the return of the blood to the heart, when it has been driven into the aorta, by the intervention of the semilunar valves) would, by a vacuum being excited each stroke of the wing, produce the desired effect, with scarcely any loss by friction.1 These elastic agents may likewise be useful in gradually stopping the momentum of large surfaces when used in any alternate motion, and in thus restoring it during their return.
Another principle, that may be applied to obviate this leverage of a wing, is that of using such a construction as will make the supporting power of the air counterbalance itself. It has been before observed, that only about one third of the wing in birds is applied in producing the propelling power; the remainder, not having velocity sufficient for this purpose, is employed in giving support, both in the beat and return of the wing.
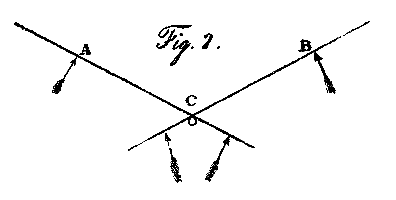
Let A and B, fig. 2, be two wings continued beyond the pole or hinge upon which they turn at C. If the extreme parts at A and B be long and narrow, they may be balanced, when in the act of skimming, by a broad extension of less length on their opposite sides; this broad extension, like the lower part of the wing, will always give nearly the same support, and the propelling part of the surface will be at liberty to act unincumbered by the leverage of its supporting power. This plan may be modified many different ways; but my intention, as in the former case, is still the principle in its simplest form.
A third principle upon which the leverage of a surface may be prevented is by giving it a motion parallel to itself, either directly up and down, or obliquely so. The surface A I, fig. 3, may be moved perpendicularly, by the shaft which supports it, down to the position K C: or, if it be supported upon two shafts with hinges at D and E, it may be moved obliquely parallel to itself into the position B L.
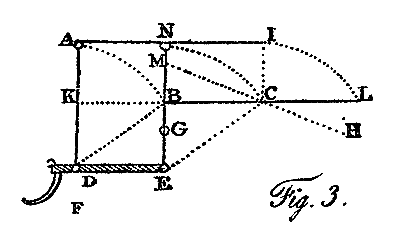
A fourth principle upon which the leverage may be greatly avoided, where only one hinge is used, is by placing it considerably below the plane of the wing, as at the point D, fig. 3, in respect to the surface A. It may be observed in the heron, which is a weak bird with an extended surface, that its wings curve downward considerably from the hinge to the tip; hence the extreme portion, which receives the chief part of the stroke, is applied obliquely to the current it creates; and thus evades in a similar degree the leverage of that portion of the supporting power, which is connected with the propelling power. These birds seldom carry their waft much below the level of the hinge of the wing, where this principle, so far as respects the supporting power, would vanish.
By making use of two shafts of unequal length, the two last mentioned principles may be blended to any required extent. Suppose one hinge to be at F, and the other at G, fig. 3, then the surface, at the extent of its beat, would be in the position of the line H M. If the surface A 1, fig. 3, be supported only upon one shaft, N E, be capable of being forced in some degree from its rectangular position in respect to the shaft, and be concave instead of flat as here represented; then the waft may be used alternately backward and forward, according to the principles of the machine I have ascribed to Mr. Degen. This construction combines the principles of counterpoising the supporting power of one part of the surface, by that of an opposite part, when the machine is in the act of skimming; and likewise the advantages of the low hinge, with the principle of leaving little or no interval without support.
All that has hitherto appeared respecting Mr. Degen's apparatus is, that it consisted of two surfaces, which were worked by a person sitting between them. This statement communicates no real information upon the subject; for scarcely any one would attempt to fly without two wings; without these being equally poised by placing the weight between them; and also, without these surfaces being capable of receiving motion from his muscular action. I may be altogether mistaken in my conjecture; my only reason for ascribing this structure of mine to Mr. Degen's machine is, that, if it were properly executed upon this principle, it would be attended with success. The drawing, or rather diagram, which is given of this machine in the first part of my essay, is only for the purpose of exhibiting the principle in a form capable of being understood. The necessary bracings, etc., required in the actual execution of such a plan, would have obscured the simple nature of its action; and were therefore omitted. The plan of its movement is also simply to exhibit, in a tangible form, the possibility of effecting the intended alternate motion of the parachutes. The seat is fronted lengthwise for the purpose of accommodating the mode of communicating the movement.
A fifth mode of avoiding leverage is by using the continued action of oblique horizontal flyers, or an alternate action of the same kind, with surfaces so constructed as to accommodate their position to such alternate motion; the hinge or joint being in these cases vertical. In the construction of large vessels for aerial navigation, a considerable portion of fixed sail will probably be used; and no more surface will be allotted, towards gaining the propelling power, than what is barely necessary, with the extreme temporary exertion of the first mover, to elevate the machine and commence the flight. In this case the leverage of the fixed surface is done away.
The general difficulties of structure in aerial vehicles, (arising from the extension, lightness, and strength required in them; together with great firmness in the working parts, and at the same time such an arrangement as exposes no unnecessary obstacles to the current,) I cannot better explain than by describing a wing, which has been constructed with a view to overcome them.
Fig. 4 represents the shape of the cloth, with a perspective view of the poles upon which it is stretched with perfect tightness. Upon the point where the rods A and B intersect is erected an oval shaft; embracing the two cross poles by a slender iron fork; for the purpose of preserving their strength uninjured by boring. To this shaft are braced the ends of the pole B, so as to give this pole any required degree of curvature. The pole A is strung like a common bow to the same curve as the pole B; and is only connected with the upright shaft by what may be called a check brace; which will allow the hinder end of this pole to heel back to a certain extent, but not the fore end. The short brace producing this effect is shown in fig. 4. Fig. 5 exhibits the fellow wing to that represented in fig. 4, erected upon a beam, to which it is so braced, as to convert the whole length of it into a hinge. The four braces coming from the ends of this beam are shown: two of them terminate near the top of the centre of the other shaft; the others are inserted into the point C, fig. 4, of the bending rod. A slight bow, not more than three eighths of an inch thick, properly curved by its string, and inserted between the hinder end of the pole A, and the curved pole C, completes the wing.
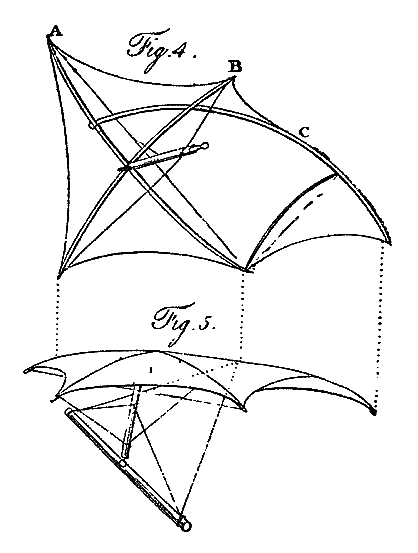
This fabrick contained 54 square feet, and weighed only eleven pounds. Although both these wings together did not compose more than half the surface necessary for the support of a man in the air, yet during their waft they lifted the weight of nine stone. The hinder edge, as is evident from the construction, being capable of giving way to the resistance of the air, any degree of obliquity, for the purpose of a propelling power, may be used.
I am the more particular in describing this wing, because it exemplifies almost all the principles that can be resorted to in the construction of surfaces for aerial navigation. Diagonal bracing is the great principle for producing strength without accumulating weight; and, if performed by thin wires, looped at their ends, so as to receive several laps of cordage, produces but a trifling resistance in the air, and keeps tight in all weathers. When bracings are well applied, they make the poles, to which are attached, bear endwise. The hollow form of the quill in birds is a very admirable structure for lightness combined with strength, where external bracings cannot be had; a tube being the best application of matter to resist as a lever; but the principle of bracing is so effectual, that, if properly applied, it will abundantly make up for the clumsiness of human invention in other respects; and should we combine both these principles, and give diagonal bracing to the tubular bamboo cane, surfaces might be constructed with a greater degree of strength and lightness, than any made use of in the wings of birds.
The surface of a heron's wing is in the ratio of 7 square feet to a pound. Hence, according to this proportion, a wing of 54 square feet would weigh about 7 3/4 pounds: on the contrary the wings of water fowl are so much heavier, that a surface of 54 square feet, according to their structure, will weigh 18 1/2 lb. I have in these instances quoted nearly the extreme cases among British birds; the wing I have described may therefore be considered as nearly of the same weight in proportion to its bulk as that of most birds.
Another principle exhibited in this wing is that of the poles being couched within the cloth, so as to avoid resistance. This is accomplished by the convexity of the frame, and the excessive lightness of the cloth. The poles are not allowed to form the edge of the wing, excepting at the extreme point of the bow, where it is very thin, and also oblique to the current. The thick part of this pole is purposely conveyed considerably within the edge. In birds, a membrane covered with feathers is stretched before the thick part of the bone of the wing, in a similar manner, and for the same purpose. The edge of the surface is thus reduced to the thickness of a small cord, that is sown to the cloth, and gives out loops whenever any fastening is required. The upright shaft is the only part that opposes much direct resistance to the current, and this is obviated in a great degree by a flat oval shape, having its longest axis parallel to the current.
The joint or hinge of this wing acts with great firmness, in consequence of its being supported by bracings to the line of its axis, and at a considerable distance from each other; n fact the bracings form the hinge.
The means of communicating motion to any surfaces must vary so much, according to the general structure of the whole machine, that I shall only observe at present, that where human muscular action is employed, the movement should be similar to the mode of pulling oars; from which any other required motion may be derived; the foot board in front enables a man to exert his full force in this position. The wings I have described were wafted in this manner; and when they lifted with a power of g stone, not half of the blow, which a man's strength could have given, was exerted, in consequence of the velocity required being greater than convenient under the circumstances. Had these wings been intended for elevating the person who worked them, they should have contained from 100 to 150 square feet each; but they were constructed for the purpose of an experiment relative to the propelling power only.
Avoiding direct resistance is the next general principle, that it is necessary to discuss. Let it be remembered as a maxim in the art of aerial navigation, that every pound of direct resistance, that is done away, will support 30 pounds of additional weight without any additional power. The figure of a man seems but ill calculated to pass with ease through the air, yet I hope to prove him to the full as well made in this respect as the crow, which has hitherto been our standard of comparison, paradoxical as it may appear.
The principle, that surfaces of similar bodies increase only as the squares of their homologous lines, while their weights, or rather solid contents, increase as the cubes of those lines, furnishes the solution. This principle is unanimously in favour of large bodies. The largest circle that can be described in a crow's breast is about 12 square inches in area. If a man exposes a direct bulk of 6 square feet, the ratio of their surfaces will be as 1 to 72; but the ratio of their weight is as I to 110; which is 1 1/2 to 1 in favour of the man, provided he were within a case as well constructed for evading resistance, as the body of the crow; but even supposing him to be exposed in his natural cylindric shape, in the foreshortened posture of sitting to work his oars, he will probably receive less resistance than the crow.
It is of great importance to this art, to ascertain the real solid of least resistance, when the length or breadth is limited. Sir Isaac Newton's beautiful theorem upon this subject is of no practical use, as it supposes each particle of the fluid, after having struck the solid, to have free egress; making the angles of incidence and reflection equal; particles of light seem to possess this power, and the theory will be true in that case; but in air the action is more like an accumulation of particles, rushing up against each other, in consequence of those in contact with the body being retarded. The importance of this subject is not less than the difficulties it presents; it affects the present interests of society in its relation to the time occupied in the voyages of ships; it will have still more effect when aerial navigation, now in its cradle, is brought home to the uses of man. I shall state a few crude hints upon this point, to which my subject has so unavoidably led, and on which I am so much interested, and shall be glad if in so doing I may excite the attention of those, who are competent to an undertaking greatly beyond my grasp.
Perhaps some approach toward ascertaining the actual solid of least resistance may be derived from treating the subject in a manner something similar to the following. Admit that such a solid is already attained (the length and width being necessarily taken at pleasure). Conceive the current intercepted or disturbed, by the largest circle that can be drawn within the given spindle, to be divided into concentric tubular laminae of equal thickness. At whatever distance from this great circle the apex of the spindle commences, on all sides of this point the central lamina will be reflected in diverging pencils, (or rather an expanding ring,) making their angles of incidence and reflection equal. After this reflection they rush against the second lamina and displace it: this second lamina contains three times more fluid than the first; consequently each pencil in the first meets three pencils in the second; and their direction, after the union, will be one fourth of the angle, with respect to the axis, which the first reflection created. In this direction these two laminae proceed till they are themselves reflected, when they (considered as one lamina of larger dimensions) rush against the third and fourth, which together contain three times the fluid in the two former laminae, and thus reduce the direction of the combined mass to one fourth of the angle between the axis and the line of the second reflection. This process is constant, whatever be the angles formed between the surface of the actual solid of least resistance at these points of reflection, and the directions of the currents thus reflected.
From this mode of reasoning, which must in some degree resemble what takes place, and which I only propose as a resemblance, it appears, that the fluid keeps creeping along the curved surface of such a solid, meeting it in very acute angles. Hence, as the experiments of the French Academy show, that the difference of resistance between the direct impulse, and that in an angle of six degrees, on the same surface, is only in the ratio of 10 to 4, it is probable, that in the slight difference of angles that occur in this instance, the resistances may be taken as equal upon every part, without any material deviation from truth. If this reasoning be correct, it will reduce the question, so far as utility is concerned, within a strictly abstract mathematical inquiry.
It has been found by experiment, that the shape of the hinder part of the spindle is of as much importance as that of the front, in diminishing resistance. This arises from the partial vacuity created behind the obstructing body. If there be no solid to fill up this space, a deficiency of hydrostatic pressure exists g within it, and is transferred to the spindle. This is seen distinctly near the rudder of a ship in full sail, where the water is much below the level of the surrounding sea. The cause here, being more evident, and uniform in its nature, may probably be obviated with better success; in as much as this portion of the spindle may not differ essentially from the simple cone. I fear however, that the whole of this subject is of so dark a nature, as to be more usefully investigated by experiment, than by reasoning; and in the absence of any conclusive evidence from either, the only way that presents itself is to copy nature; accordingly I shall instance the spindles of the trout and woodcock, which, lest the engravings should, in addition to the others, occupy too much valuable space in your Journal, must be reserved to a future opportunity.